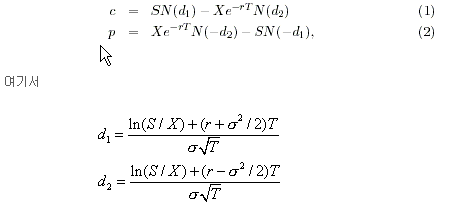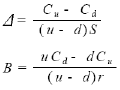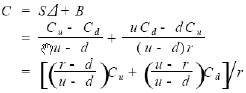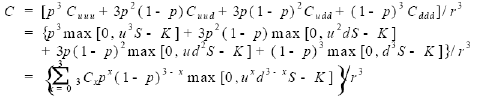1) 블랙-숄즈 모형
① 기본 개념
- 옵션의 가치를 기초자산인 주식가격과 시간의 함수로 가정하고 주식투자와 옵션거래를 적당히 배합한 무위험 포트폴리오를 만든 후 그것의 수익을 무위험 채권투자와 같은 것으로 놓아 도출되는 미분방정식 형태로써 옵션가격이 시간의 진행에 따라 어떻게 변화되는지 나타냄
② 모형의 의의
- 파생상품의 정상가격이 어떻게 결정되는지 수학적으로 보여줌으로써 경험과 직관에만 의존하던 판단기준을 보다 객관적이고 과학적으로 만들었음 - 파생상품의 발행자에게 발행에 따른 위험을 분석 가능케 함으로써 위험에 대한 보호책을 제시가능하게 하였음 - 무배당 주식에 대한 유럽형 옵션 가격을 구하는데 유용함 - 주식옵션이 아닌 다른 옵션가격에도 광범위하게 적용할 수 있음
③ 모형의 문제점
- 만기에만 행사가능한 유럽식 주식 옵션을 대상으로 개발되었기 때문에 미국식 옵션 평가에는 한계가 있음 - 중도에 배당금 지불이나 주가의 돌발적인 변화가 발생하면 적용하기 힘들게 됨
④ 모형의 형태
- c와 p를 각각 유럽형 콜옵션과 풋옵션의 가격이라고 하면 블랙-숄즈 공식은 아래와 같음
이고, S는 주식가격, X는 옵션의 행사가격, r는 무위험이자율, T는 옵션의 잔존만기(연 단위), ?는 기초자산의 변동성, N(x)는 누적정규분포함수임
2) 이항분포 모형
① 기본 개념
- 기초자산인 주가의 변화가 상승과 하락의 두가지 형태로만 나타날 경우 옵션의 위험헤지 포트폴리오의 구성을 통해 이론가격을 계산하는 모형
② 모형의 의의 및 특징
- 아주 간단한 가정만 하고서도 옵션가치를 계산할 수 있음 - 주가가 3번이상 변화하더라도 일반화 할 수 있음 - 옵션의 가격은 주가가 오를 확률이나 내릴 확률과는 무관함 - 옵션의 가격은 투자자의 위험에 대한 태도와 무관함 - 콜옵션 가격을 결정하는데 있어서 유일한 확률변수는 주가이며 옵션 행가가격(K), 옵션확률, 이자율, 만기가 같다면 옵션가격은 동일한 값을 가짐 - 옵션가격결정모형은 투자자들의 위험에 대한 태도나 미래에 대한 동일한 예측을 필요로 하지 않음 (자본자산결정모형(CAPM)에서는 투자자들이 위험회피자라고 가정하고 미래에 대해 동일한 예측을 한다고 좀더 엄격한 가정을 함)
③ 모형의 형태
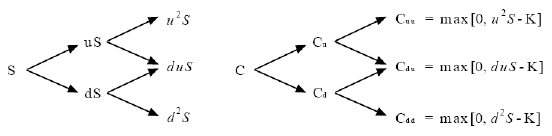
ⓐ 1기간 이항모형
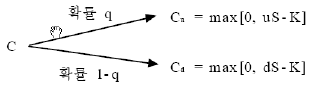
: 행사가격 K이고 잔존만기가 1기간 남은 콜옵션의 현재가치를 C라 하고 1기간 후 주가가 uS로 상승했을 때의 콜옵션 가치를 CU, 주가가 dS로 하락했을 때 콜옵션 가치를 Cd 라 하면 CU, Cd 는
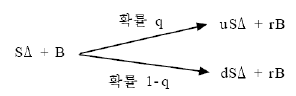
: 주식 Δ개와 $B 상당의 무위험채권으로 구성된 포트폴리오를 구성한다고 가정하면 포트폴리오의 구성비용은 SΔ + B 이며 무위험 이자율 채권의 이자율을 rf 라 할때 r = 1+ rf 라고 하면 1기간 후 포트폴리오는 아래와 같음
: 1기간 후 포트폴리오 가치가 콜옵션과 같기 위해서는 아래의 관계식이 성립되어야 함
: 이로부터 Δ, B를 구하면
: 무위험 차익거래 기회가 없으려면 콜옵션의 현재가치가 포트폴리오의 구성비와 동일해야 하므로 아래의 식이 도출됨
: p ≡ (r-d)/(u-d) 이라 하면, 1-p ≡ (u-r)/(u-d) 이므로 위식은 다음과 같이 단순화 시킬 수 있음
ⓑ 2기간 이항모형
- 1기간 이항모형을 확장한 형태로서 u, d가 모든 기간에서 일정하고 각 기간의 길이도 일정하다고 가정하기 때문에 주가 S는 1기간마다 S에 u를 곱한 가격으로 상승하거나 d를 곱한 가격으로 하락한다고 하면, 아래와 그림에서와 같이 2기간 이항모형에서 주가는 3가지로 변화 가능함 (CUU 는 주가가 2기간 연속 상승시 콜옵션 가치를, Cdd 는 주가가 2기간 연속 하락시 콜옵션 가치 나타냄)
- u, d가 모든 기간에서 일정하므로 p = (r-d)/(u-d)도 모든 기간에 일정하게 되어 아래식과 같게 되며
- 아래식에 대입하게 되면
- 최종적으로 콜옵션은 다음과 같이 구하게 됨
- 동적헷지 비율도 구할 수 있는데 아래와 같음
ⓒ 다기간 이항모형
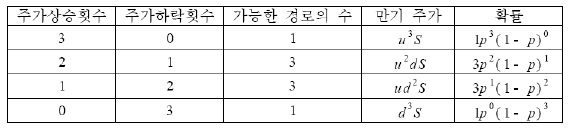
- 3기간 주가 상승 확률
- 3기간 이항 모형
- n기간 이항모형
- x<a 이면 max[0, uxdn-x S-K] =0 이고 x≥a 이면 max[0, uxdn-x S-K] = uxdn-x S-K 가 되므로
- 2부분으로 나누면
- 간단히 아래와 같이 정의하면
- p′ ≡ (u/r)p 라 하면 1- p′ = (d/r)(1-p) 이며 아래의 식을 도출할 수 있음
- 최종적으로 아래 식이 도출되며 블랙-숄즈 공식과 사실상 같은 형태임
|