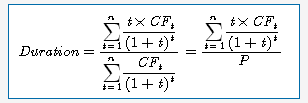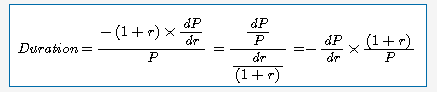1) 개념

듀레이션이란 채권에서 발생하는 현금흐름을 각각 발생하는 기간으로 가중하여 현재 가치한 합을 채권의 가격으로 나눈 것이며, 이는 채권에 투자된 원금의 평균회수기간이라고 할 수 있음

[n=만기까지의 이자지급횟수, t=현금흐름 발생기간, CFi=채권에서 발생하는 각 기의 현금흐름, r=채권만기수익률, P=채권의 가격]

2) 특징

① 만기시 일시상환채권의 듀레이션은 이 채권의 잔존기간과 동일

② 이표채의 듀레이션은 이 채권의 잔존기간보다 작음

③ 이표채의 표면이율이 높을수록 듀레이션이 작아짐

④ 채권의 시장만기수익률이 높을수록 듀레이션은 작아짐

⑤ 일반적으로 잔존기간이 길수록 듀레이션은 커짐

3) 듀레이션과 채권가격

듀레이션은 다음과 같이 수익률변동에 대한 채권가격의 민감도 개념으로 표현됨

또한, 위식에서 듀레이션이 주어질 때 수익률의 변동에 따른 채권가격의 변동율의 관계는 아래와 같이 표현될 수 있음.

여기에서의 우항의 을 수정듀레이션이라고 함

4) 듀레이션의 한계와 볼록성

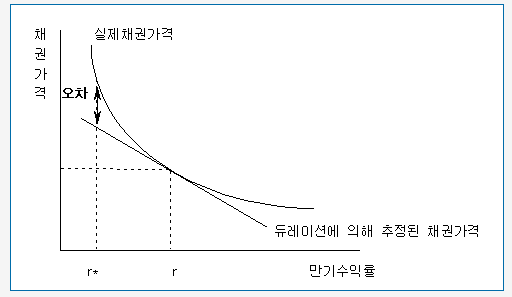
수익률 변동에 의한 채권가격변동을 추정하는 데 사용되는 듀레이션은 채권가격 결정요인들에 대한 포괄적 정보를 포함하는 유용한 개념임.

그러나 듀레이션을 이용하여 추정된 채권가격의 변동은 수익률 변동폭이 작은 경우에는 실제 가격변동과 큰 차이가 없으나, 수익률 변동폭이 커질수록 실제 가격변동치와 비교해 오차가 증가하는 경향이 있음.

이와 같은 결과가 나오는 것은 일반적으로 실제 채권가격과 만기수익률은 원점에 대하여 볼록한 곡선모양을 갖는 데 비해, 듀레이션을 이용하여 추정된 채권가격과 만기수익률의 관계는 듀레이션 산출의 기준이 되는 만기수익률을 접점으로 선형관계를 보이기 때문임

따라서 듀레이션에 의한 가격변동 산출에서 발생하는 추정오차 축소가 필요하며 이는 볼록성의 개념을 통해 가능해짐